Egy épülő csarnok keresztmetszete a következő harmadfokú függvénnyel írható le:
ahol b a fél szélesség (12 m), h a gerinc magassága (10 m).
A csarnok hosszúsága l (20 m), az álmennyezetet magassága m (7 m).
Egy lehetséges megoldás: LETÖLTÉS
1. feladat
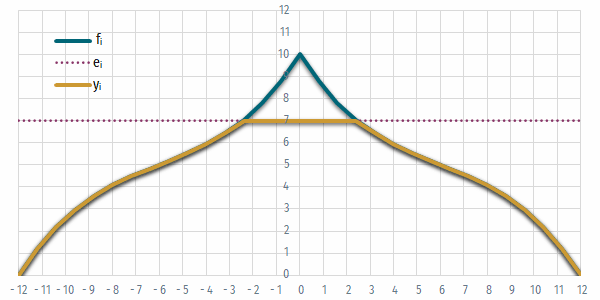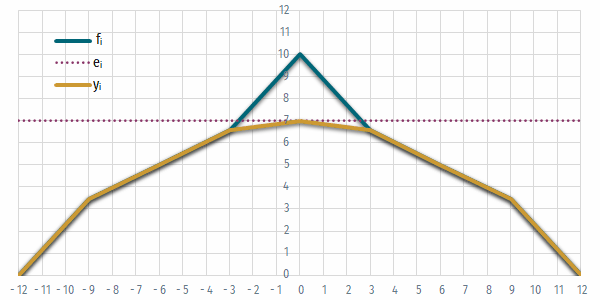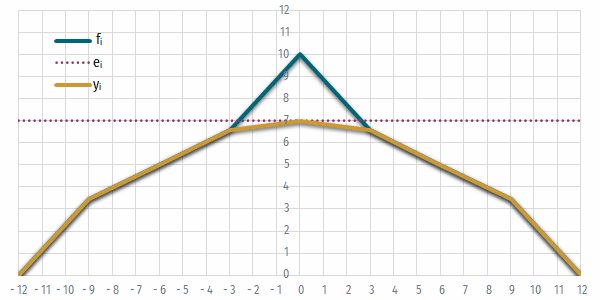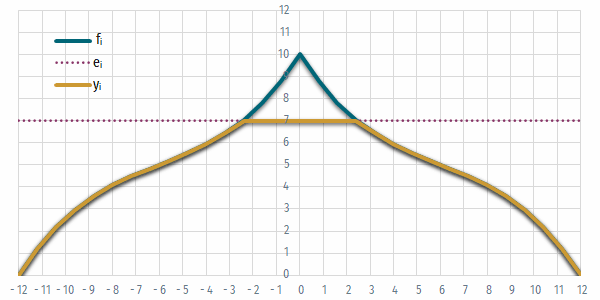
- Ábrázoljuk a csarnok keresztmetszetét, kiemelve az álmennyezet alatti részt!
• Matematikai háttér
Az ábrázolni (és számítani) kívánt görbét kisebb szakaszokra osztjuk, az egyes szakaszokon a görbét húrjával helyettesítjük, és mind a görbe felrajzolását, mind pedig a terület és ívhossz számítását ezen közelítés alapján végezzük el.
A b fesztávolságot kiindulásul 2n számú egyenlő részre osztjuk, hogy minden n érték esetén legyen olyan pont, ami a szimmetriatengelyre esik. A görbe ábrázolásakor x irányban végighaladunk –b-től +b-ig a teljes fesztávolságon, és minden i lépésnél kiszámítjuk a függvény magassági koordinátáit.
A valós görbe osztáspontjainak egyenes szakaszokkal való összekötésével egy vonallánc adódik. Általános helyen, a tetszőleges i-edik lépésnél a vonallánc egy elemi szakaszának vízszintes koordinátái xi és xi+1, míg magassági koordinátái yi és yi+1 lesznek.
• Görbe ábrázolása
Definiáljuk a szükséges geometriai paramétereket!
- Egy cellát (B3) nevezzük el b-nek (fél szélesség), értéke legyen 12.
- Egy cellát (C3) nevezzük el h-nak (magasság), értéke legyen 10.
- Egy cellát (D3) nevezzük el m-nek (magasság), kezdeti értéke legyen 7.
- Egy cellát (E3) nevezzük el l-nak (hosszúság), értéke legyen 20.
Hozzuk létre a táblázatban az értelmezési tartomány x értékeit!
A görbe megjelenítésének (és számításának) pontosságát meghatározza, hány pontban számoljuk ki a függvény értékét. Mivel ez esetben a függvény szimmetrikus, érdemes páros számú (2n) szakaszra osztani. A felosztáshoz érdemes egy hagyományosan i-vel jelölt „számláló” értéket alkalmazni, amely az egyes osztáspontok sorszámát jelzi –n-től +n-ig (-10 ≤ i ≤ +10). Az i sorszámú pont x koordinátáját ekkor az i/n*b képlettel kapjuk.
- Egy cellát (A3) nevezzük el n-nek és értékének írjunk mondjuk 10-et.
- Hozzunk létre egy számsort –n-től +n-ig az A oszlopban!
=SORSZÁMLISTA(2*n+1;;-n) =SEQUENCE(2*n+1;;-n) - Nevezzük el az A5# tartományt _i-nek!
- A B oszlopba, az i számsor első eleme mellé számítsuk ki x értékeit!
=_i/n*b - Nevezzük el a B5# tartományt _x-nek!
Hozzuk létre a táblázatban az értékkészlet tartomány y értékeit!
- A C oszlopba, x első eleme mellé írjuk be a fenti függvény képletét:
=h/4*(2+(1-ABS(_x)*2/b)^3+(1-ABS(_x)*2/b)) - Nevezzük el a C5# tartományt _f-nek!
- Az ábra szemléletessebbé tétele érdekében a D oszlopba írjuk be az álmennyezet vízszintes egyenesének képletét:
=m+_i-_i (az i-re való hivatkozás csak azt szolgálja, hogy ez az oszlop is dinamikus legyen) - Az E oszlopba írjuk be a belső tér kontúrját kiszámoló képletet: =IF(_f<m; _f; m)
- Nevezzük el az E5# tartományt _y-nak!
Ábrázoljuk a csarnok keresztmetszetét!
- Jelöljük ki az B5:E55 tartományt!
- Válasszuk a Beszúrás Insert menüben a Diagramok Charts csoportból a Pont vonalakkal Scatter with Straight Lines típust!
- Mivel az ábra tengelyei nem automatikusan arányosak, érdemes az x és y tengelyek maximum értékét azonosra állítani, és a diagram osztásainak arányát négyzetesre igazítani.
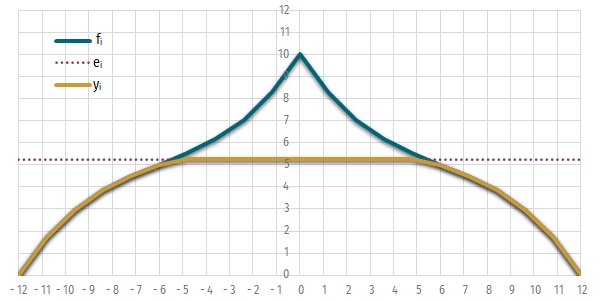
2. feladat
- Határozzuk meg a végfal és a tető csatlakozási vonalának ívhosszát, és a végfal területét!
- Határozzuk meg, hogy az álmennyezet milyen m magassága esetén lenne pontosan 2000 m³ a csarnok térfogata!
• Matematikai háttér
Két szomszédos osztáspont között a görbét húrjával közelítve e szakasz alatti ∆ter területrész trapéznak tekinthető:
Két szomszédos osztáspont között a görbét húrjával közelítve e szakasz ∆ív hossza egy olyan derékszögű háromszög átfogójaként adódik, amelynek vízszintes befogója a két x koordináta, függőleges befogója pedig a két y koordináta különbsége:
Ezen elemi ívhosszakat és területeket minden szakaszra vonatkozóan kiszámítva, majd valamennyi szakaszra összegezve a teljes ívhossz és terület műszaki szempontból kielégítő pontosságú közelítését kapjuk.
• Ívhossz és terület számítása
Számítsuk ki a csarnok végfalának ívhosszát, és keresztmetszetének területét!
Fontos figyelni arra, hogy a szakaszok darabszáma mindig eggyel kisebb az osztáspontokénál, ezért mindig eggyel kevesebb elemi ívhossz és terület szerepelhet, mint ahány koordináta értéket kiszámoltunk. Mivel az i-edik szakaszhoz szükséges az i+1-edik osztáspont is, az i=n esetben már nem számolhatunk sem ívhosszt, sem területet.
- A képletek könnyebben érthetővé, áttenkinthetőbbé tehetők, ha definiáljuk az xi+1 és yi+1 koordinátákat tartalmazó tartományokat a Névkezelő (Name Manager, Ctrl+F3) segítségével, mint az eredeti tartományok „függőlegesen eltolt” verzióit:
_xa =OFFSET(_x;1;0)),
_ya =OFFSET(_y;1;0)). - Az ívhossz és a terület képletei a korábban matematikai alakban megadott ∆ív és ∆ter képletek „fordításai”:
∆ter =IF(_i=n; ""; (_xa - _x) * (_ya + _y) /2)
∆ív =IF(_i=n; ""; SQRT( (_xa - _x)^2 + (_ya - _y)^2 ) ) - Számítsuk ki a teljes keresztmetszeti területet és ívhosszt:
=SUM(F5#)
=SUM(G5#) - Nevezzük el a területet ∑Ter-nek!
• Egyenlet megoldása
Határozzuk meg a keresett térfogatot eredményező álmennyezet-magasságot iterációval!
- Számítsuk ki a csarnok térfogatát a keresztmetszeti terület és a hosszúság szorzataként:
=∑Ter*l - Nevezzük el ezt a cellát V-nek!
- Válasszuk a Adatok Data menüben a Adateszközök Data Tools csoportból a Lehetőségelemzés • Célértékkeresés What-If Analysis • Goal Seek lehetőséget!
- A célcella set cell értelemszerűen a V térfogat.
- A célérték to value a feladat szerinti 2000.
- A módosuló cella by changing cell a feladat értelmében az m magasság.
Az gomb megnyomása után a program megkeresi m azon értéket, mely esetén V értéke közelítőleg 2000-re adódik.
Alaposabban megnézve a diagramot látható, hogy némi pontatlanság keletkezik abból, hogy a két függvény metszéspontja nem valamelyik osztáspontnál adódik. A felosztás n értékét növelve ez a pontatlanság természetesen csökkenthető (vagy ha nem akarunk túl sok ponttal dolgozni, az összemetsződés helye újabb iterációval pontosítható), így megkereshető, hogy az f és m közötti magassági különbség x milyen értékénél lesz elegendően pontosan 0.
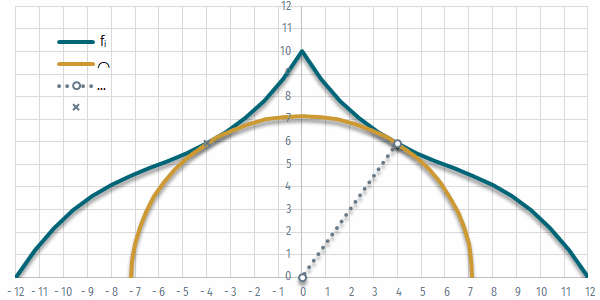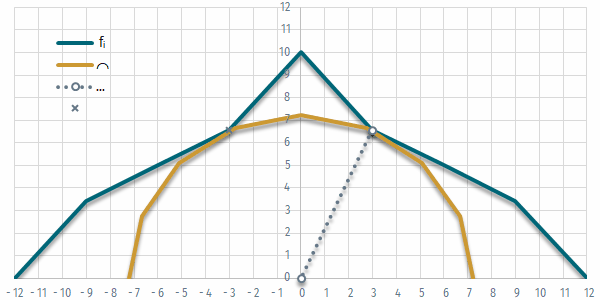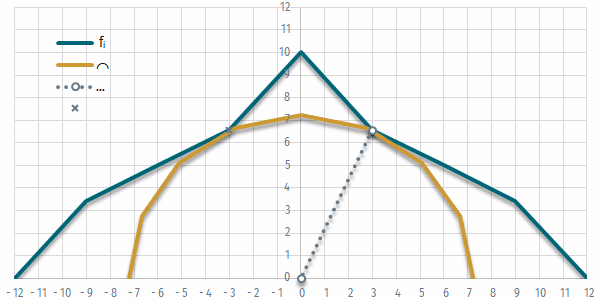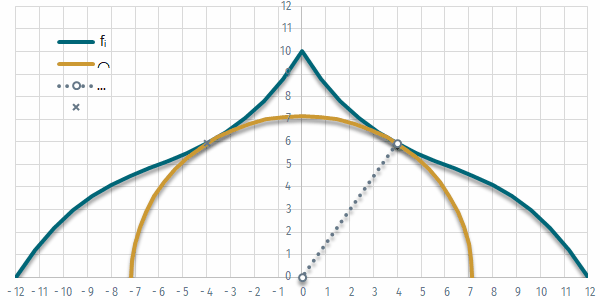
3. feladat
- Ábrázoljuk a csarnok keresztmetszetét, és az azt érintő [0,0] középpontú félkört!
• Matematikai háttér
A félkör sugarát növelve „hozzáér” a függvényhez – pontosabban a függvény azon pontjához, amely legközelebb esik az origóhoz. Ezen érintési pont origótól való távolsága adja a keresett félkör sugarát. Első közelítésben csak a függvény ábrázolásakor használt osztáspontok közül keressük a legközelebbit – később pontosabb megoldást is keresünk.
A harmadfokú görbe esetén x szerint számoltuk az y értékeket egyenletes Δx lépésköz mellett. A félkör esetén ez a megoldás kissé nehézkes és pontatlan lenne, így pontjainak x és y értékekét ρ függvényében számoljuk, az osztáspontokhoz tartozó középponti szöget egyenletesen léptetve. Jelen esetben a 0 és π közötti tartományt kell felosztani 2n részre, minden osztáspontban kiszámítva ρ aktuális értékét, illetve az ahhoz tartozó x és y koordinátákat.
Az origó középpontú félkör paraméteres egyenletrendszere:
ahol
• Görbe ábrázolása
Definiáljuk a szükséges geometriai paramétereket!
- Egy cellát (K2) nevezzük el rᵨ-nek,
kezdeti értéke legyen pl. 6.
(Az r az angol Excelben a sort jelöli, ezért nem alkalmas névnek.) - A H oszlopba, _i első eleme mellett számítsuk ki ρ értékeit 0-tól π-ig
=SORSZÁMLISTA((2*n+1;;0) / (2*n) * PI() ⇄ =SEQUENCE(2*n+1;;0) / (2*n) *PI() - Nevezzük el a H5# tartományt ρ-nak!
Számoljuk ki a félkör osztáspontjainak koordinátáit!
- A J oszlopba, ρ első eleme mellett számítsuk ki x értékeit
=rᵨ*COS(_ρ) - Nevezzük el a J5# tartományt _xᵨ-nak!
- A K oszlopba, ρ első eleme mellett számítsuk ki y értékeit
=rᵨ*SIN(_ρ) - Nevezzük el a J5# tartományt _yᵨ-nak!
Ábrázoljuk a csarnok keresztmetszetét!
- Hozzuk létre az előbbihez hasonló módon a csarnok keresztmetszetét ábrázoló diagramot, vagy módosítsuk az előzőt úgy, hogy csak az _f függvényt mutassa!
- A félkör hozzáadásához a diagram aktív állapotában elérhető Diagramtervezés ⇄ Chart Design fülön válasszuk az Adatok kijelölése ⇄ Select Data ikont!
- Adjuk meg a görbe nevét, az xᵨ (J5:J55) és yᵨ (K5:K55) értékek tartományát!
A félkör sugarát kössük az eredeti függvény legközelebbi osztáspontjához!
- A H oszlopban számoljuk ki a harmadfokú görbe osztáspontjainak távolságát az origótól:
=(_x^2+_f^2)^(1/2) - Nevezzük el a H5# tartományt _d-nek!
- Az rᵨ cellában a konstans helyett használjuk a számított távolság-értékek közül a legkisebbet:
=MIN(_d)
Pontosabb értéket n növelésével, a Solver segítségével, vagy Visual Basic modullal kaphatunk.
• Szélsőérték meghatározása Solver segítségével
A függvény tetszőleges pontjának távolságának origótól vett távolsága egyszerűen meghatározható:
A távolság így felírható egy olyan függvényként, ahol y a fenti harmadfokú függvény. Ennek az új függvénynek a minimumértéke az érintő kör sugara. Egy folytonos függvény helyi szélsőértéke (minimuma vagy maximuma) olyan pontban lehet, amelyben adifferenciálhányados zérus, vagy nem létezik (például végtelenné válik). Geometriai értelemben a függvény szélsőértéke ott van, ahol a függvény meredeksége (az adott pontban rajzolt érintőjének meredeksége) zérus, illetve azon két pont között, ahol a meredekség előjelet vált.
A Solver egy telepíthető modul, mely iterációval határozza meg a szélsőértéket. Amennyiben már aktiválva van, az Adatok ⇄ Data menüben a Solver ponttal érhetjük el. Ha itt nem szerepel, próbáljuk meg betölteni (Office Súgó)
A félkör sugarát kössük az eredeti függvény legközelebbi osztáspontjához!
- Nevezzünk el egy cellát xs-nek, értéke legyen mondjuk 3!
- Nevezzünk el egy másik cellát ys-nek:
=h/4*(2+(1-ABS(xs)*2/b)^3+(1-ABS(xs)*2/b))! - Számítsuk ki az rᵨ cellában az [xs,ys] pont távolságát az origótól:
=(xs^2+ys^2)^(1/2)! - Hívjuk be a Solver párbeszéd-ablakát!
- Minimumértéket keresünk, ezért kattintsunk a Cél: sorban a Min választógombra!
– a Célérték beállítása mezőbe írjuk be az rᵨ cellahivatkozást – e cella minimumértékét keressük
– a Változócellák módosításával mezőbe írjuk az xs cellahivatkozást – e cella értékét fogja iterálni a program
– végül nyomjuk meg a gombot!
A keresett érték pontossága a Solver Beállítások párbeszédablakban beállított paraméterektől függ – most elfogadhatjuk az alapértékeket.
Ha sikeres a keresés, akkor a A Solver eredményei párbeszédablak jelzi, hogy a Solver talált egy (lehetséges) megoldást, amelynél minden megszorítás és optimálási feltétel teljesült, és ekkor választhatunk, hogy megtartjuk a talált értéket (A Solver megoldásának megtartása), vagy visszatérhetünk az eredeti értékekhez (Eredeti értékek visszaállítása).
Ha a Solver nem talál a megszorításoknak és az optimálási feltételeknek teljesülő megoldást, A Solver nem talált létező megoldást üzenet jelenik meg.
A megoldás vizuális ellenőrzésére érdemes a szélsőérték-kereséssel kapott pont megjelenítése pontként, vagy pl. az origóval összekötött szakaszként.