The cross-section of a hall can be described by the following function:
where b is the half-span (12 m) and h is the height (10 m).
The length of the hall is l (20 m), the height of the false ceiling is m (7 m).
A possible solution: DOWNLOAD

Task 1
- Depict the cross-section of the hall and highlight the part under the false ceiling.
• Mathematical background
Let's divide the curve of the function into smaller sections, replacing the curve with its chord at each of these sections, and use this approximation to draw and calculate its enclosed area and length.
Let's divide the span into 2n equal parts which ensures that for every n value there is a point that falls on the symmetry axis. When plotting the curve, we move in the x direction from –b to +b over the entire span, and at each i step we calculate the height as the yvalue of the function.
Connecting these points of the original curve with straight segments results in a polyline. At an arbitrary i step, the horizontal coordinates of the endpoints of the current segment are xi and xi+1 , while its height coordinates are yi and yi+1.
• Plotting the curve
Defining the geometric parameters
- Name a cell (B3) as b (half-span) and set its value to 12.
- Name a cell (C3) as h (height) and set its value to 10.
- Name a cell (D3) as m (height) and let its initial value be 7.
- Name a cell (E3) as l (length) and set its value to 20.
Calculating the x values
The accuracy of the representaiton of the curve is determined by the number of points in which the value of the function is calculated. Since in this case the function is symmetrical, it is worth dividing it into an even number of sections (2n). We can use a variable traditionally denoted by i for indicating the sequence number of each point from –n to +n (-10 ≤ i ≤ +10). The x coordinate of the point i is then obtained by the formula i/n*b.
- Name a cell (A3) as n (number of segments) and set its value to 10.
- Create a sequence of numbers from –n to +n in column A:
=SEQUENCE(2*n+1;;-n) - Name the A5# range as _i.
- In column B, next to the first element of the series i, calculate the values of x:
=_i/n*b - Name the B5# range as _x.
Calculating the y values
- In column C, next to the first element of x, enter the formula for the above function:
=h/4*(2+(1-ABS(_x)*2/b)^3+(1-ABS(_x)*2/b)) - Name the C5# range as _f.
- In column D, enter the formula of the horizontal straight line of the suspended ceiling:
=m+_i-_i (the reference to i makes this column dynamic too) - In column E, calculate the contour of the interior:
=IF(_f<m; _f; m) - Name the E5# range as _y.
Depicting the cross-section
- Select the range B5:E55.
- In the Insert menu, in the Charts group select the Scatter with Straight Lines chart type.
- Since the figure is not automatically proportional, set the maximum values of the x and y axes to the same value and adjust the ratio of the chart.
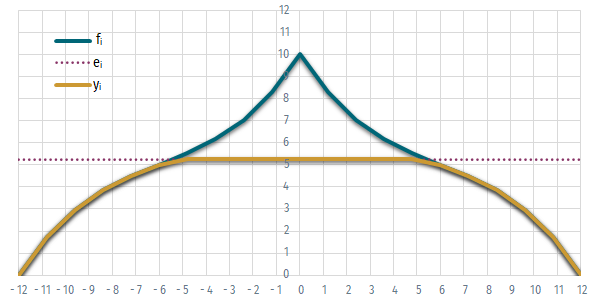
Task 2
- Determine the arc length of the outline of the wall and the area of the wall.
- Determine what height m of the suspended ceiling would ensure that the volume of the hall is exactly 2000 m³.
• Mathematical background
When we substitute the curve with its string between two division points, the area ∆a below section i can be calculated as a trapezoid:
When we substitute the curve with its string between two division points, the length ∆l of section i can be obtained as the hypotenuse of a right-angled triangle and the lengths of its legs can be calculated as the difference between the two x and the two y coordinates:
By calculating these elementary arc lengths and areas for each section and summing them up, we obtain an approximation of the total arc length and area with satisfactory accuracy.
• Calculations
Calculating the arc length and the area
It is important to note that the number of sections is always one less than that of the division points, so there can always be one less elementary arc length and area than the number of coordinate values calculated. Since the section i requires division point i+1 also, in the case of i=n we can no longer calculate either the ∆l length or ∆a area.
- The formulas can be made easier to enter and understand by defining the domains containing the xi+1 and yi+1 coordinates.
We can use the Name Manager (Ctrl+F3) to define the “vertically shifted” versions of the original domains:
_xa =OFFSET(_x;1;0)),
_ya =OFFSET(_y;1;0)). - The formulas of the arc length and area are simple translations of the above mathematical formulas:
=IF(_i=n; ""; (_xa - _x) * (_ya + _y) /2)
=IF(_i=n; ""; SQRT((_xa - _x)^2 +(_ya - _y)^2 )) - Calculate the total cross-sectional area and arc length:
=SUM(F5#)
=SUM(G5#) - Name the area as ∑Area.
• Solving an equation
Determining the suspended ceiling height
- Calculate the volume of the hall by multiplying the area of the cross-section by the length:
=∑Area*l - Name the area as V.
- In the Data menu, in the Data Tools group select the What-If Analysis • Goal Seek command.
- The set cell should obviously be the volume V.
- The to value should be 2000.
- The by changing cell should be the height m.
- Press OK, and the program tries to find the value of m for which V is approximately equal to 2000.
A closer look at the diagram shows that some inaccuracies arise from the fact that the intersection of the two functions is not exactly in a division point. By increasing the n number of the division, this inaccuracy can of course be reduced (or, if you don't want to work with too many points, the intersection location can be refined with iteration)—you can find what x belongs to a point where the height difference between f and m is sufficiently close to zero.

Task 3
- Plot the cross-section of the hall and a semicircle which is tangential to it and has its center at the [0,0] point.
• Mathematical background
If we increase the radius of the semicircle it obviously reaches the point of the function that is closest to its center point, the origin. The distance of this point of contact from the origin decides the radius of the semicircle. As a first approximation, we can look for the closest point that has been used in the representation of the function — later we will look for a more precise solution.
For the third-degree curve, the y values were calculated for each x value with an even increment of Δx. In the case of a semicircle, this solution would be somewhat cumbersome and imprecise, so both the x and the y coordinates are calculated as functions of ρ, the central angle of the points. To get an even increment of Δρ, we divide the range 2n times from 0 to π, and for each ρ value we calculate the x és y coordinates.
The parametric equations of a semicircle whose center is at the origin:
where
• Plotting the curve
Defining the geometric parameter
- Name a cell (K2) as rρ (the semicircle's radius) and let its initial value be 6 (r represents the row in English Excel).
Calculating the coordinates
- In column B, next to the first element of the series i, calculate the values of angle ρ from 0 to π:
=SEQUENCE(2*n+1;;0) / (2*n) *PI() - Name the H5# range as _ρ.
- In columns J and K, next to the first element of the series ρ, calculate the values of x and y:
=rρ*COS(_ρ)
=rρ*SIN(_ρ) - Name the J5# range as _xρ.
- Name the K5# range as _yρ.
Depicting the semicircle
- Create a diagram of the cross-section the same way as above, or modify the previous one to show only the _f function.
- In order to add the semicircle, activate the Chart Design tab which is available while the chart is active and click on the Select Data icon.
- Enter the name of the curve and specify the _xρ and _yρ ranges.
Depicting the radius
- In column H, calculate the distance between the points of the curve from the origin:
=(_x^2+_f^2)^(1/2) - Name the H5# range as _d.
- Modify rρ so that it shows the smallest of the calculated distance values:
=MIN(_d)
You can get a more accurate value by increasing n, by using Solver, or by using a Visual Basic module.
• Determining the extreme value
The distance from the origin can be determined quite simply for any point of the curve:
The distance can thus be written as a new function and the minimum value of this new function determines the radius of the tangent circle. In geometric terms, the extreme value of a function is where the slope of the function (the slope of its tangent drawn at that point) is zero and between the two points where the slope changes its sign.
Solver is a module in Excel that can use iteration to determine the extreme value. If it is already activated, you can access it from the Data menu. If it's not there, try to load it (see the Office Help)
Using the Solver to find the tangent point
- Name a cell as xs and set its value to e.g. 3.
- Name another cell as ys and calculate its value:
=h/4*(2+(1-ABS(xs)*2/b)^3+(1-ABS(xs)*2/b))! - In the rρ cell calculate the distance of the point [xs,ys] from the origin:
=(xs^2+ys^2)^(1/2)! - Start the Solver.
- Select the Min option in the Target: row.
- In the Set target value field, enter the rρ since we are looking for the minimum value of that cell.
- In the Change variable cells box type the xs reference since this this cell should be iterated.
- and press the Solve button.
If the search is successful, the Solver Results dialog box indicates that it has found a possible solution where all constraints and optimization condition has been met, and then we can choose to keep the Solver solution), or you can restore the original values).
In order to visually check the solution, it is worth showing the location of the tangent point e.g. by plotting the line connecting it with the origin.