⭳ összes kinyitása ⭱ összes becsukása

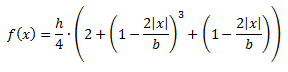
Egy csarnok metszete a következő harmadfokú függvénnyel írható le:
 – ahol b a fél fesztáv (6,00 m),
 – h a gerincmagasság (7,00 m).

1. Ábrázoljuk a csarnok metszetét!
2. Határozzuk meg, hogy a (b²/6 + (x + h/6)²)^½ függvény mely pontban metszi a kontúrt!

Egy lehetséges megoldás |↷|      

1. Függvényábrázolás |↷|

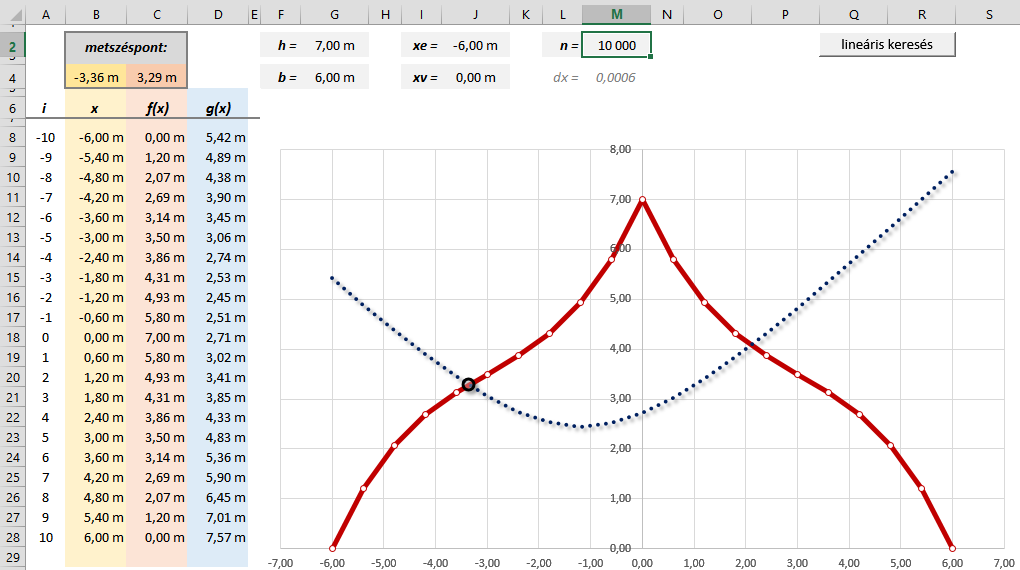
Ábrázoljuk a csarnok keresztmetszetét, illetve az azt metsző függvényt.

1.1 Előkészítés, paraméterek

• A G2 cellát nevezzük el h-nak és értékének írjunk 7-et.
• A G4 cellát nevezzük el b-nek és értékének írjunk 6-ot.

1.2 Értelmezési tartomány

Mivel a függvény szimmetrikus, érdemes páros számú (2n) szakaszra osztani – n legyen 10.

A felosztáshoz érdemes egy i segédváltozót alkalmazni, amely az egyes osztáspontok sorszámát jelzi –n-től +n-ig (-10 ≤ i ≤ +10).

Az egyes pontok x koordinátáját az i/n·b képlettel kapjuk meg. ⥯ Hogyan?

1.3 Értékkészlet

• A C oszlopba, x első eleme mellé (C8 cella) írjuk be a csarnok kontúrjának képletét! ⥯ Hogyan?
=h/4*(2+(1-ABS(x)*2/b)^3+(1-ABS(x)*2/b))
• A D oszlop ugyanazon sorába (D8 cella) írjuk be a fenti függvény képletét! ⥯ Hogyan?
=(b^2/6+(x+h/6)^2)^(1/2)
• Másoljuk le a képletet minden x mellé!

1.4 Görbe felrajzolása

• Jelöljük ki az B8:D28 tartományt!
• Válasszuk a Beszúrás ⇄ Insert menüben a Diagramok ⇄ Charts csoportból a Pont vonalakkal ⇄ Scatter with Straight Lines típust!
• Mivel az ábra nem arányhelyes, érdemes az x és y tengelyek maximum értékét azonosra állítani, és a diagram arányát nagyjából négyzetesre igazítani.
• Érdemes lehet még hozzáadni harmadikként a metszéspont helyét megadó mpx és mpy pontokat tartalmazó „függvényt”, ami majd megmutatja az átmetszésként azonosított pontot.

2. Metszéspontkeresés |↷|

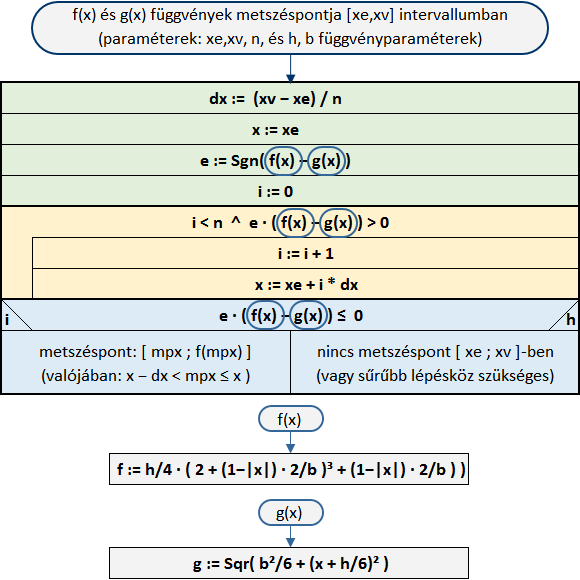
Keressük meg a két függvény metszéspontját az itt látható algoritmusnak megfelelő programmal, az intervallum 10 000 részre osztásával.

2.1 Előkészítés, paraméterek

• A J2 cellát nevezzük el xe-nak és értékének írjunk -b-t.
• A J4 cellát nevezzük el xv-nek és értékének írjunk 0-át.
• A M2 cellát nevezzük el n-nek és értékének írjunk 10 000-et.
• A B4 cellát nevezzük el mpx-nek („metszéspont”).
• A C4 cellát nevezzük el mpy-nak, és másoljuk oda az f(x) képletet.
• Az M4 cellát nevezzük el dx-nek (egyelőre üresen maradhat).

2.2 VBA indítása

Válasszuk a Fejlesztőeszközök ⇄ Developer menüben a Kód ⇄ Code csoportból a Visual Basic lehetőséget, majd a megjelenő ablak bal oldali panelében kattintsunk a VBAProject (Fájlnév) részén jobb egérgombbal, és válasszuk az Insert ⇨ Module parancsot.

♦ Ha a szalagmenüben nem látható a Fejlesztőeszközök ⇄ Developer menü, akkor a Fájl ⇄ File menü Beállítások ⇄ Options parancsára megjelenő panel Menüszalag testreszabása ⇄ Customize Ribbon lapján a jelölőnégyzetben jelöljük be, hogy látható legyen.

2.3 Függvények definiálása

Definiáljuk a h és b paramétereket mint globális változókat, illetve az f(x) és g(x) függvényeket. ⥯ Hogyan?

' [D1] globális változók definiálása:
    Dim h, b As Double
' [F1] f(x) függvény definiálása:
  Function f(x As Double)
    Let f = h / 4 * (2 + (1 - Abs(x) * 2 / b) ^ 3 + (1 - Abs(x) * 2 / b))
  End Function
' [F2] g(x) függvény definiálása:
  Function g(x As Double)
    Let g = Sqr(b ^ 2 / 6 + (x + h / 6) ^ 2)
  End Function

2.4 Paraméterek beolvasása

A [D1] definíciók után (a függvények definíciója elé) szúrjuk be az új szubrutint. ⥯ Hogyan?

• Mindenekelőtt definiáljuk az f(x) és g(x) függvényeknek átadni kívánt x paramétert.
• A táblázatban elnevezett cellákra ugorva olvassuk ki az xe, xv, n, h, b változók értékeit.

Sub linker() 
' két függvény metszéspontjának lineáris keresése
' [D2] függvények paramétereként átadandó változó definiálása:
    Dim x As Double
' [V1] változók értékének átvétele a táblázatból:
  Application.Goto Reference:="xe"
    Let xe = ActiveCell.Value   ' « intervallum eleje
  Application.Goto Reference:="xv"
    Let xv = ActiveCell.Value   ' « intervallum vége
  Application.Goto Reference:="n"
    Let n = ActiveCell.Value    ' « intervallum-osztáspontok száma
  Application.Goto Reference:="h"
    Let h = ActiveCell.Value    ' « függvény „h” paramétere
  Application.Goto Reference:="b"
    Let b = ActiveCell.Value    ' « függvény „b” paramétere
End Sub

2.5 Változók kezdőértékének számítása

Az End Sub parancs elé szúrjuk be azokat az értékadásokat, melyek segítségével megtörténhet majd a metszéspont keresése. ⥯ Hogyan?

• Számítsuk ki a keresés osztásközét az xe és xv közötti távolság n részre osztásával!
• Állítsuk a vizsgált pont x koordinátáját a keresési intervallum elejére (xe)
• Állítsuk a csomópontokat számláló i változót 0-ra.
• Tároljuk el a két függvény kezdeti magassági viszonyát e segédváltozóként: Szignum( f(x) – g(x) ).

' [V2] változók kezdeti értékének számítása:
    Let dx = (xv - xe) / n      ' « keresési osztásköz számítása
    Let x = xe                  ' « keresési kezdőpont felvétele
    Let i = 0                   ' « segédváltozó a csomópontok számlálásához
    Let e = Sgn(f(x) - g(x))    ' « függvények helyzete az intervallum elején

2.6 Metszéspont keresése

Az End Sub parancs elé szúrjuk be a metszéspont keresését szolgáló ciklust. ⥯ Hogyan?

• A ciklus magjának minden lefutásakor a csomópontokat számláló i segédváltozó értékét kell növelni eggyel, majd kiszámolni ezen új csomópont x koordinátáját.
• A ciklus futását valójában a Do While sor szabályozza, amelyik a mag minden lefutása előtt ellenőrzi, hogy fenáll-e két feltétel. Az első feltétel, hogy még nem értük el az intervallum végét – azaz i még kisebb, mint n. A másik feltétel, hogy a két függvény közül még mindig az legyen felül, amelyik a futtatás kezdetén – amit úgy ellenőrizhetünk, hogy e előjele egyezik-e az f(x)–g(x) különbségnek az épp vizsgált pontabn számolt előjelével (mely esetben szorzatuk nagyobb lesz nullánál).

' [L1] metszéspont keresése 
  Do While i < n And e * (f(x) - g(x)) > 0
    Let i = i + 1               ' « segédváltozó léptetése
    Let x = xe + i * dx         ' « vizsgálat helyének léptetése
  Loop                          ' « új [L1] ciklus indítása

2.7 Eredmények kiírása

Az End Sub parancs elé szúrjuk be a programunk eredményét a táblázatba visszaíró programrészt. ⥯ Hogyan?

• A táblázatban elnevezett cellákra ugorva írjuk be a dx osztásköz, illetve (ha van átmetszés) a metszéspont mpx koordinátájának értékeit.
• Amennyiben nincs átmetszés, erről üzenetben tájékoztassuk a használót.

' [RE] eredmény kiíratása üzenetként illetve a táblázatba:
    Application.Goto Reference:="dx"
      ActiveCell.FormulaR1C1 = dx
  If e * (f(x) - g(x)) <= 0 Then
    Application.Goto Reference:="mpx"
      ActiveCell.FormulaR1C1 = x
  Else: MsgBox ("Nincs metszéspont az intervallumban," & _
      Chr(10) & "vagy dx = " & dx & " nem elegendően sűrű lépésköz.")
    Application.Goto Reference:="mpx"
      ActiveCell.FormulaR1C1 = "0"
  End If

2.8 Futtatás és kiértékelés

A program indítása többféleképp történhet.

• Választhatjuk a Fejlesztőeszközök ⇄ Developer menüben a Kód ⇄ Code csoportból a Makrók ⇄ Macros lehetőséget, majd a megjelenő panelen kiválasztva a makró nevét, az Inditás ⇄ Start) gombot.
• Ha többször akarjuk futtatni a makrót, érdemes lehet ugyanezen menüben a Vezérlők ⇄ Controls csoportból a Beszúrás ⇄ Insert gomb alatti Gomb ⇄ Button lehetőséget választani, amivel egy gombot helyezhetünk el a táblázatban, amelyre kattintva azután egyszerűbben elindítható a hozzá rendelt makró (javasolt temészetesen a gomb feliratát átírni).

A program jelen formájában addig fut, amíg meg nem történik az átmetszés, vagyis amíg már nem az eredetileg fölül lévő függvény van fölül. Elvileg előfordulhat, hogy éppen olyan pontot vizsgálunk, ahol a két függvény értéke egyenlő, és ebben az esetben a metszéspont pontos helyét kapjuk eredményül. Sokkal valószínűbb azonban, hogy túllépünk a metszésponton, és ilyenkor csak annyit tudhatunk biztosan, hogy a valódi átmetszés távolsága kisebb, mint a dx osztásköz. (Ha például az n lépésszámot 10-re állítjuk, dx osztásköz 0,6 m lesz, miáltal az átmetszés mpx koordinátájaként -3,0 m adódik – a valós „hiba” tehát ~0,36 m.)

BME Morfológia és Geometriai Modellezés Tanszék