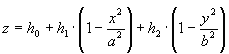
Számítógépek alkalmazása 1 |
2002/2003. év - I. félév |
Térfogatszámítás | |
A gyakorlat témája: Héjfelületek ábrázolása, felszín- és térfogatszámítása az táblázatkezelővel.
A gyakorlat folyamán különböző, héjszerkezetű lefedéseknél használatos felületek ábrázolását, felszínük kiszámítását, és az általuk határolt beépített térfogat meghatározását fogjuk elvégezni. Tanulmányozzuk továbbá, hogy a héjfelületek megadásánál szereplo paraméterek miként befolyásolják a héj alakját, felszínét és a beépített térfogatot.
Egy transzlációs felületet fogunk ábrázolni, illetve a térfogatát valamint a felszínét számítjuk ki.
| A felületet a | 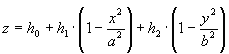 |
képlet írja le. |
| A felületet a | és | téglalap alaprajz felett kívánjuk ábrázolni. |
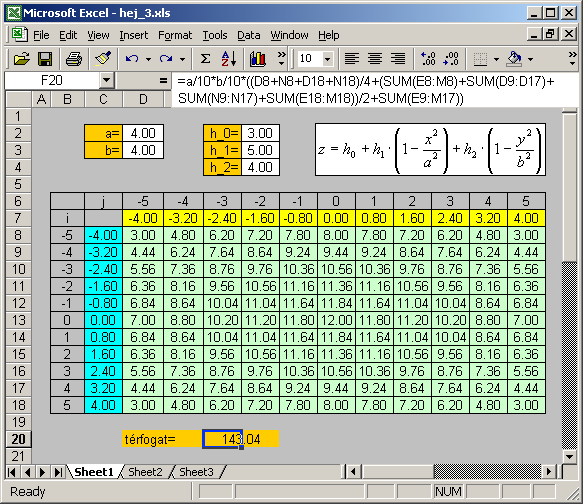
A felületek ábrázolása (valamint a felület és a köbtartalom közelíto számítása) ugyanúgy a véges kis részekre való felosztás elvén (a diszkretizáláson) alapul, mint ahogyan ezt síkgörbék esetében már láttuk. Osszuk fel tehát mindkét alaprajzi koordináta irányban az a ill. b fél fesztávolságot 5 - 5 részre. Természetesen, ha több részre osztjuk, pontosabb eredményt kapunk. Ezzel az xy síkon egy derékszögű négyszögháló alakul ki. A háló a metszéspontjaiban kiszámítjuk a z magassági koordinátákat. Ezek segítségével ábrázoljuk és számítjuk ki a felület felszín illetve a felület alatti térfogat közelítő értékét.
1. Előkészítés, paraméterek definiálása
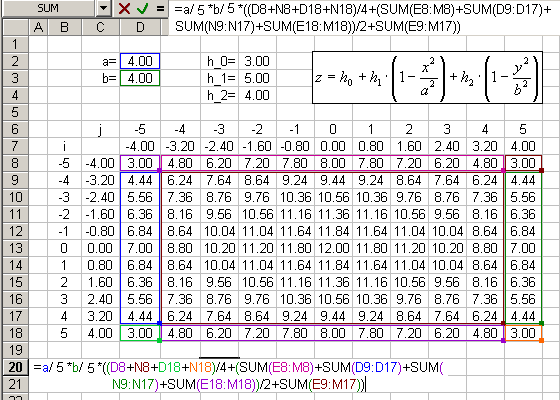
Definiáljuk a paramétereket, a-t és b-t, valamint h_0, h_1 és h_2 paramétereket!
2. Értelmezési tartomány generálása
A magassági értékek kiszámításához elő kell állítani az x és y koordináták sorát. Először a hálópontok sorszámát állítjuk elő -5-től +5-ig:
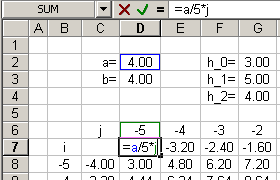 |
Beírjuk az első cellába az =a/5*j képletet majd lemásoljuk egymás mellé! (A cellán állva az [F2] billentyűvel ellenőrizhetők a hivatkozások.) |
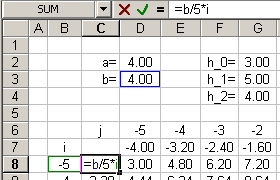 |
Beírjuk az első cellába az =b/5*i képletet majd lemásoljuk egymás alá! (A cellán állva az [F2] billentyűvel ellenőrizhetők a hivatkozások.) |
3. Értékkészlet előállítása
Írjuk be a =h_0+h_1*(1-x^2/a^2)+h_2*(1-y^2/b^2) képletet az első cellába
(ellenőrizzük a hivatkozásokat az [F2] billentyűvel),
majd másoljuk azt a teljes sorba, végül a sort másoljuk le egymás alá!
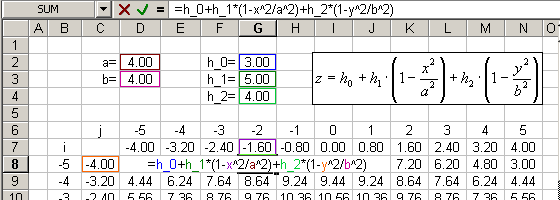
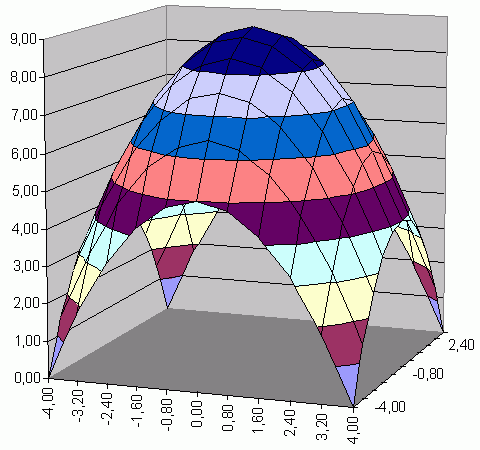
4. Függvényábrázolás
Jelöljük ki a teljes tartományt az x, y értékekkel együt:
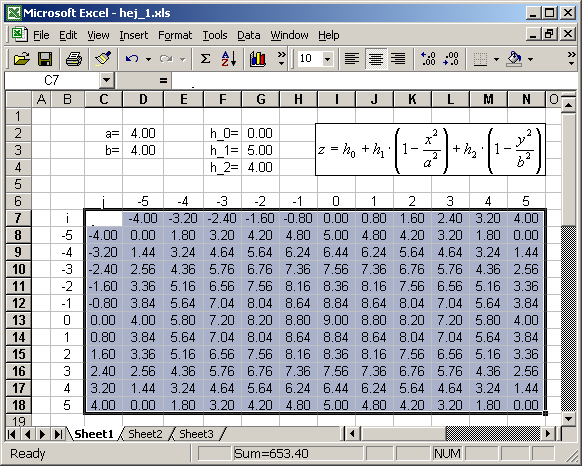
A Diagram varázslóban (Chart Wizard) ![]() válasszuk ki a felület/Surface típust:
válasszuk ki a felület/Surface típust:
A párbeszéd ablak gombjával továbbléphetünk, vagy (mivel amúgy is megfelelnek az alapbeállítások) a gombbal befejezhetjük a beállításokat.
5. Térfogatszámítás
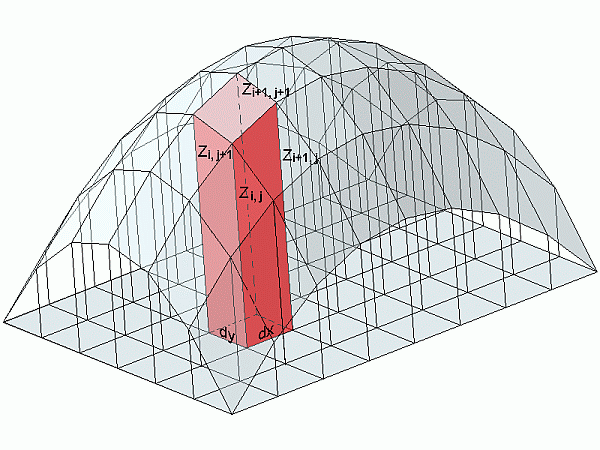
A kiszámított z értékek segítségével felírhatjuk az elemi hasábok térfogatát:
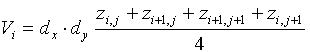
A teljes térfogat:
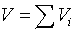
Erre készíthetünk egy új táblázatot, de kifejtve az összegzést, kiemelhetjük a hasábok alapterületét (dx*dy), hiszen jelen esetben ez állandó. A kiemelés után azt láthatjuk, hogy minden általános helyen lévő z értéket egyszeres, minden peremen lévő z értéket fél, a sarkokon lévő z értéket negyed súllyal kell figyelembe venni.
Így felírva:
6. Felszínszámítás
A felszínszámításnál a diszkretizálás alkalmazásához kapcsolódó számítási egyszerrusítés abban áll, hogy a görbe felület szóbanforgó kis darabját két háromszöglappal helyettesítjük, s e síkidomok területe elemi úton számítható. A háromszög területét a
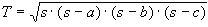 összefüggés alapján számíthatjuk, ahol a, b, c a háromszög oldalai, s a fél kerület:
összefüggés alapján számíthatjuk, ahol a, b, c a háromszög oldalai, s a fél kerület:
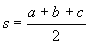
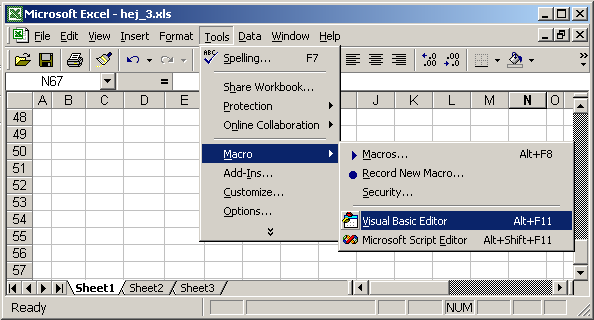
A felszínszámítás elve egyszerű, gyakorlati megvalósítása tisztán táblázat segítségével kicsit körülményes, ezért újabb eszközt használunk. Ez pedig a beépített Visual Basic editorral készített saját függvény. Hívjuk be a Visual Basic editort a Tools/Macro/Visual Basic Editor menüponttal:
Hozzunk létre egy új modult az Insert/Module menüponttal:
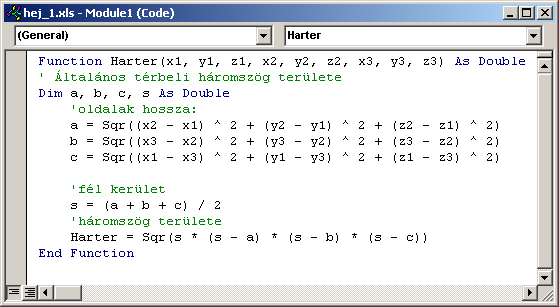
Először egy általános térbeli háromszög területét kiszámoló függvényt készítünk a fenti összefüggések alapján. Paraméterei a háromszög sarokpontjainak koordinátái, azaz [x1,y1,z1],[x2,y2,z2],[x3,y3,z3]
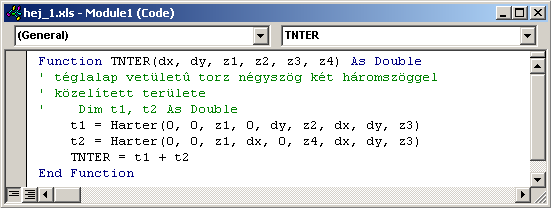
A könnyebb adatmegadás miatt készítsünk egy speciális függvényt, amivel elkerülhetjük, hogy a vetületi téglalap felett keletkező torz négyszöget helyettesítő két háromszöghöz 18 - részben azonos - adatot kelljen megadni. A függvényünk paraméterei dx, dy, z1,z2,z3,z4 amelyek az elemi hasáb alaplapjának méretei, illetve a sarokpontok z koordinátái(az óramutató járásának megfelelően). Így a tizennyolc paraméter helyett csak hatot kell megadni. E függvény "meghívja" az általános térbeli háromszög területét kiszámító függvényt (harter) és "visszaadja" a háromszögek területét.
Az így elkészített függvényeket a beépített függvényekhez hasonlóan tudjuk használni.
Írjuk be a felszínszámításhoz használt tartomány bal felső cellájába a TNTER függvényt, átadva a dx (a/5), dy (b/5), valamint az elemi hasáb sarokpontjainak z koordinátáit! (Ellenőrizzük a hivatkozásokat az [F2] megnyomásával!)
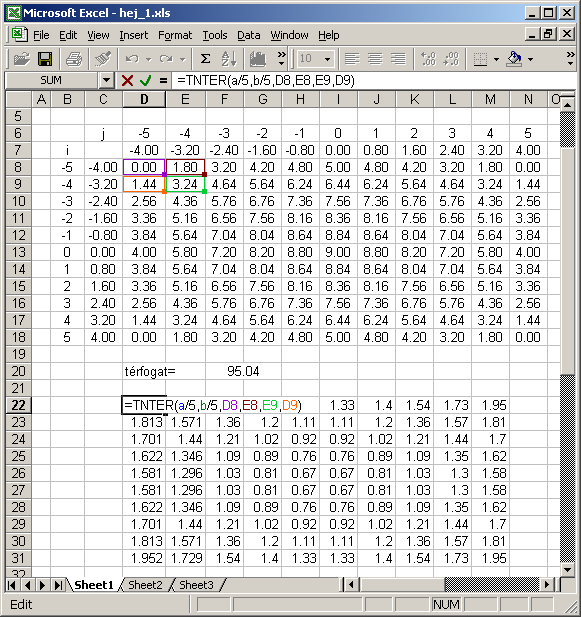
Másoljuk le a szokásos módon. figyeljünk arra, hogy egy sorral és egy oszloppal kevesebb helyre másoljuk, mint amennyi z értékünk van a felső táblázatban! (Ellenőrizzük a hivatkozásokat az [F2] megnyomásával!)
Adjuk össze a kapott torznégyszögek (két háromszög) területét a SUM függvénnyel!
7. Formázás
A számítás után formázhatjuk a táblázatot: