Számítógépek alkalmazása |
|
2005/2006. tanév - I. félév |
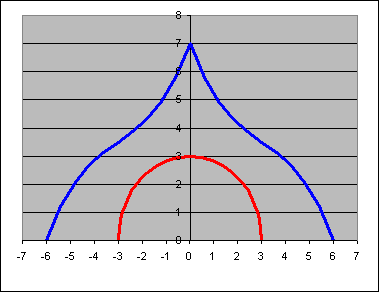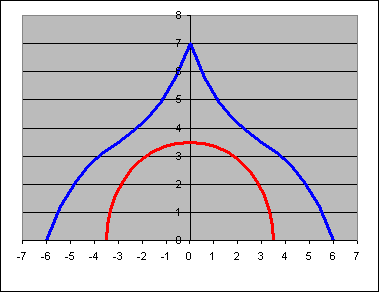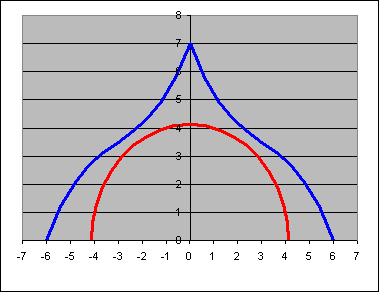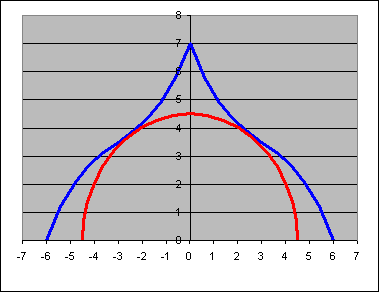
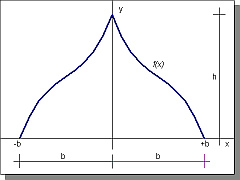
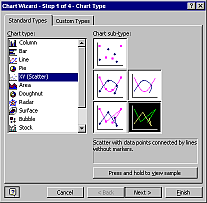
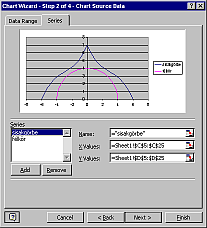
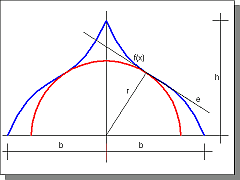
A gyakorlat témája: Ábrázoljuk az alábbi képlettel leírható harmadfokú függvényt, és egy 0,0 origójú félkört, melyek érintik egymást. A képlet:
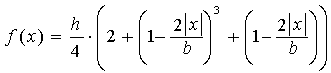
A félkör sugarát növelve egyszercsak "hozzáér" a függvényhez, egészen pontosan a függvény azon pontjához, amely a legközelebb esik az origóhoz. Ez a pont lesz az érintési pont, origótól való távolsága pedig a keresett félkör sugara. Meg kell tehát keressük a harmadfokú függvény origóhoz legközelebb eső pontját!
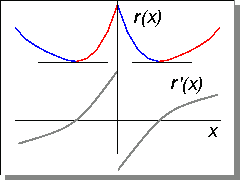
Írjuk fel a függvény egy általános pontjának távolságát az origótól:
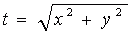
Ezzel egy újabb függvényt kaptunk, ahol y a fenti harmadfokú függvényünk. Ennek az új függvénynek a minimumértéke lesz az érintő kör sugara.
Egy folytonos függvény helyi szélsőértéke (minimuma vagy maximuma) olyan pontban lehet, amelyben a differenciálhányados zérus, vagy nem létezik (például végtelenné válik).
Geometriai értelemben a függvény szélsőértéke ott van, ahol a függvény meredeksége (az adott pontban rajzolt érintőjének meredeksége) zérus, illetve azon két pont között, ahol a meredekség előjelet vált.
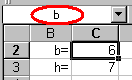
Nevezzük el a C2 cellát b-nek (ezentúl így hivatkozunk rá),
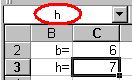
majd nevezzük el a C3 cellát h-nak!
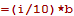 képlettel kapjuk meg.
képlettel kapjuk meg.
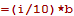 képletet!
képletet!
 képletet!
képletet!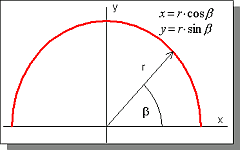
A harmadfokú görbénél x szerint írtuk fel az y értékeket egyenletes dx mellett. A kört b szerint írjuk fel, azaz b értékeit kell előállítani 0-tól p radiánig.
A kör paraméteres egyenletrendszere (ha a kör középpontja [0,0]):
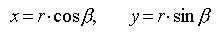 , ahol
, ahol 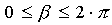
Az ábrán látható félkör értelmezési tartománya:
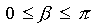
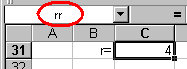
Mivel az r név az angol Excelben a sort jelenti (s így nem használható névként), nevezzük a sugarat rr-nek, (ezentúl így hivatkozunk rá). Kezdeti értéknek írjunk a cellába 4-et!
Az osztáspontok sorszáma 0-tól megy 20-ig azaz 0 <= i <= 20.
Az adott sorszámú b értékét a 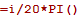 képlettel kapjuk meg.
képlettel kapjuk meg.
 képletet!
képletet!
 képletet!
képletet!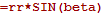 képletet!
képletet!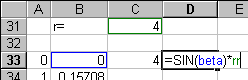
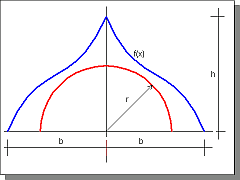
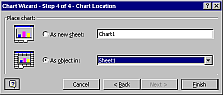
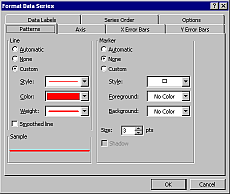
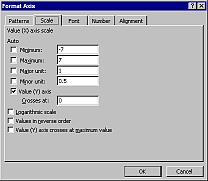
írjuk fel az E oszlopba harmadfokú görbe első pontja mellé a pont távolságát az origótól a =GYÖK(x^2+y^2) (angolul SQRT) képlettel, majd másoljuk le a képletet egymás alá az összes pont mellé! Ellenőrizzük grafikusan a távolság függvényt (készítsünk ideiglenes diagramot a Diagram varázslóval): látható, hogy van szélsőérték!
Írjuk be az rr cellába a =MIN(E9:E29) képletet!
(Pontosabb értéket a Solverrel, vagy egyedi Visual Basic modullal számíthatunk.)
A Solver az Excel alá telepíthető modul, mely iterációval határozza meg a szélsőértéket.
Amennyiben installálva és aktiválva van, a Solvert Tools • Solver menüponttal érhetjük el. Ha itt nem szerepel, próbáljuk aktiválni a Tools • Add-Ins… menüpont panelén – ha itt sem látható, nincs telepítve!
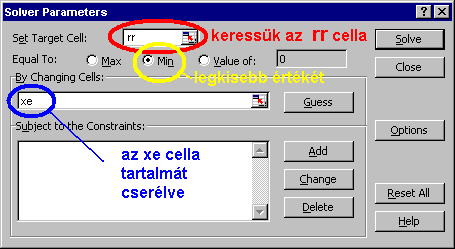
Minimumértéket keresünk, ezért aktiváljuk az Equal To: sorában a Min rádiógombot!
A Set Target Cell mezőbe írjuk be az rr cellahivatkozást: e cella minimumértékét keressük.
A By Changing Cells: mezőbe írjuk az xe cellahivatkozást: e cella értékét fogja cserélgetni a Solver.
Végül nyomjuk meg a gombot!
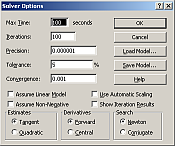
A keresett érték pontossága a Solver Options (Beállítások) dialógusablakban beállított paraméterektől függ. Most elfogadhatjuk az alapértékeket.
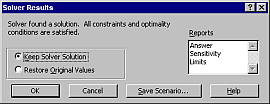
Ha sikeres a keresés, akkor a Solver Results párbeszédablak jelzi, hogy a Solver talált egy (lehetséges) megoldást, amelynél minden megszorítás és optimálási feltétel teljesült, és ekkor választhatunk, hogy megtartjuk a talált értéket (Keep Solver Solution), vagy visszatérhetünk az eredeti értékhez (Restore Original Values).
(Amennyiben a Solver nem talál a megszorításoknak és az optimálási feltételeknek teljesülő megoldást, a Solver could not find a feasible solution. üzenet jelenik meg)
Irodalom:
(c)2005. BME Építészeti Ábrázolás Tanszék